Obs: Aqui encontrarão as principais áreas e volumes das mais comuns figuras planas.
Área é um conceito matemático que pode ser definida como quantidade de espaço, ou seja, de superfície.
De acordo com SI (Sistema Internacional de medidas) o metro é considerado a unidade principal de medida de comprimento, seguido de seus múltiplos e submúltiplos. Os múltiplos do metro são o quilômetro (Km), hectômetro (hm) e decâmetro (dam) e os submúltiplos são decímetro (dm), centímetro (cm) e milímetro (mm). Entre as medidas são estabelecidos critérios de conversão, de acordo com a tabela a seguir:
.jpg)
A medida que as unidades seguem a orientação da direita os valores são multiplicados por 10. E a medida que seguimos a orientação para a esquerda os valores são divididos por 10. Essa tabela de conversão existe para que os valores estejam sempre na mesma unidade. vamos realizar as seguintes transformações:
Exs:
- 10 Km em metros : 10 x 10 x 10 x 10 = 10.000 metros
- 7 hm em dam : 7 x 10 = 70 decâmetros
- 5 m em cm : 5 x 10 x 10 = 500 centímetros
- 4 km em mm : 4 x 10 x 10 x 10 x 10 x 10 x 10 = 4.000.000 milímetros
Onde: A é a área e l o seu lado.
Ex::
01. A tampa de uma caixa mede 17cm. Qual á superfície desta tampa ?
Logo l = 17cm, substituindo na fórmula temos :
A = 17 x17
A = 289cm²
02. A medida do lado de um quadrado é 20cm. Qual é sua área ?
Logo, l = 20cm, substituindo:
A = 20²
A = 400cm²
Onde; b é a base e h a altura.
Ex :
01. Um terreno medi 5m de largura por 25m de comprimento. Qual é a área deste terreno?
Temos: b = 25m e h = 5m, substituindo na fórmula:
A = 25 x 5
A = 125m²
02. A tampa de uma caixa de sapatos tem as dimensões 30cm e 15cm. Qual é sua área ?
Temos: b = 30cm e h 15cm, substituindo:
A = 30 x 15
A = 450cm²
Onde: b é a base e h altura.
Ex:
01. A medida da base de um triângulo é de 7cm, visto que a medida de sua altura é de 3,5cm. Qual é a área deste triângulo?
Temos: b = 7cm e h 3,5cm, substituindo:
A = 7 x 3,5 / 2
A = 12,25cm²
Onde: B é a base maior, b a base menor e h a altura.
Ex:
01. Calcule a área de um trapézio, cujo suas medidas são, 40cm e 20cm de base e 10cm de altura.
A= 40 + 20 x 10/2
A = 600/2
A = 300cm²
A = a x h
Onde: a base e h altura.
Onde: D é a diagonal maior e d a diagonal menor.
Ex :
01. Se as duas diagonais de um losango medem, respectivamente, 6cm e 8cm, então a área do losango é:
Temos: D = 8cm e d = 6, substituindo:
A= 8 x 6 / 2
A = 48/2
A = 24cm²
Onde: r é o raio e d o diâmetro.
Ex:
01. Calcule a área do circulo que tem como raio 3cm.
Temos: r = 3cm, substituindo:
A= π x 3²
A = 9πcm²
VOLUME
Volume de um corpo é a quantidade de espaço ocupada por esse corpo. Volume têm as unidades de medidas cúbicas( cm³,m³, in³,etc).
| Volume | Capacidade |
|---|
| Metro cúbico | Quilolitro |
| Decímetro cúbico | Litro |
| Centímetro cúbico | Mililitro |
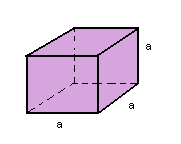
V = a³
Ex :
01. O volume de um cubo é de 8cm³, então quanto vale o comprimento de seus lados?
8 = a³
a = 
a = 2cm
V = a x b x c
V = A x h
Onde: A é a área da base e h a altura.
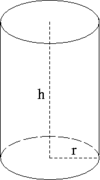
V = πr²h
Onde: r é o raio de uma face circular e h a altura.
Onde: b é a base e h a altura .
Onde: r é o raio da esfera.
Onde: r é o raio do circulo na base e h a altura.
V = 
Enfim, terminamos aqui nosso assunto, lembrando que abordamos apenas as principais figuras dentre as várias existente.
Fonte :



.jpg)












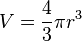


.jpg)
Nota 10
ResponderExcluirÓtimo 😍
ResponderExcluirMuito bom obrigado
ResponderExcluirmuito bom
ResponderExcluirBOA PIVETE
ResponderExcluir